11719. Reduce the array

Given an array of n integers and an integer k. Find the minimum cost to reduce the array to a single element. You can perform the following operation any number of times:

· Choose any pair of consecutive elements a_i and a_i+1, and replace them with (a_i + a_i+1). The cost of this operation is k * (a_i + a_i+1).

Input. The first line contains two integer n and k (n, k ≤ 100). The second line contains n integers a₁, a₂, …, a_n (0 ≤ a_i ≤ 100).

Output. Print the minimum cost to reduce the array to a single element.

Sample input 1	Sample output 1
3 2 1 2 3	18
Sample input 2	Sample output 2
4 3 4 5 6 7	132

SOLUTION

dynamic programming

Algorithm analysis

Let f(i, j) represent the minimum cost to reduce the subarray [a_i, …, a_j] to a single element. This value will be stored in the cell dp[i][j].

Obviously, f(i, i) = 0.

From the problem statement, it follows that

f(i, i + 1) = k * (a_i + a_i+1)

Now, let’s compute f(i, i + 2). Reducing three numbers into one can be done in two ways:

· Merge a_i and a_i+1 with a cost of k * (a_i + a_i+1), then merge a_i + a_i+1 and a_i+2 at a cost of k * (a_i + a_i+1 + a_i+2).

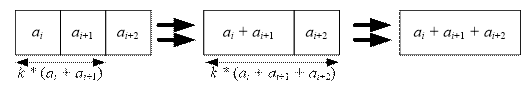
· Merge a_i+1 and a_i+2 with a cost of k * (a_i+1 + a_i+2), then merge a_i and a_i+1 + a_i+2 at a cost of k * (a_i + a_i+1 + a_i+2).

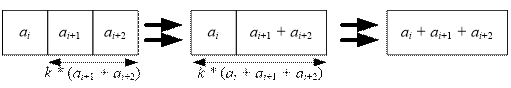
Thus f(i, i + 2) =

min(k * (a_i + a_i+1) + k * (a_i + a_i+1 + a_i+2), k * (a_i+1 + a_i+2) + k * (a_i + a_i+1 + a_i+2))

Now, let’s consider calculating the value of f(i, j). To reduce the subarray [a_i, …, a_j] to a single element equal to a_i + …+ a_j, we need to choose some value p (i ≤ p < j). Then, recursively solve the problem for the subarrays [a_i, …, a_p] and [a_p+1, …, a_j], and finally merge the elements a_i + … + a_p and a_p+1 + … + a_j. The value of p should be chosen in such a way that the total transformation cost is minimized:

f(i, j) =

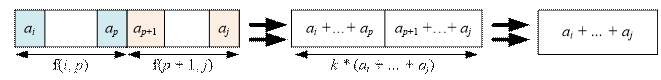
For efficient computation of sums a_i + …+ a_j, use a prefix sum array pref, where

pref[i] = a₁ + …+ a_i,

so that a_i + …+ a_j = pref[j] – pref[i – 1] .

Algorithm implementation

Let’s declare constants and arrays.

#define MAX 101

#define INF 0x3F3F3F3F

int dp[MAX][MAX], a[MAX], pref[MAX];

The function f(i, j) returns the minimum cost to transform the subarray [a_i, …, a_j] into a single element.

int f(int i, int j)

{

if (dp[i][j] == INF)

for (int p = i; p < j; p++)

dp[i][j] = min(dp[i][j], f(i, p) + f(p + 1, j) +

(pref[j] - pref[i - 1]) * k);

return dp[i][j];

}

The main part of the program. Read the input data.

scanf("%d %d", &n, &k);

memset(dp, 0x3F, sizeof(dp));

for (i = 1; i <= n; i++)

{

scanf("%d", &a[i]);

dp[i][i] = 0;

Compute the array of prefix sums.

pref[i] = pref[i - 1] + a[i];

}

Compute and print the answer.

printf("%d\n", f(1, n));

Python implementation

Let’s declare the constant for infinity.

INF = float('inf')

The function f(i, j) returns the minimum cost to transform the subarray [a_i, …, a_j] into a single element.

def f(i, j):

if dp[i][j] == INF:

for p in range(i, j):

dp[i][j] = min(dp[i][j], f(i, p) + f(p + 1, j) +

(pref[j] - pref[i - 1]) * k)

return dp[i][j]

The main part of the program. Read the input data.

n, k = map(int, input().split())

a = [0] + list(map(int, input().split()))

Compute the array of prefix sums.

pref = [0] * (n + 1)

for i in range(1, n + 1):

pref[i] = pref[i - 1] + a[i]

Initialize the dp array.

dp = [[INF] * (n + 1) for _ in range(n + 1)]

for i in range(1, n + 1):

dp[i][i] = 0

Compute and print the answer.

print(f(1, n))